BOOLEANO

El término “sistema booleano” salió el último día en la materia, asique debido a mi nulo conocimiento en este ámbito, me decidí a investigar un poco en ello.

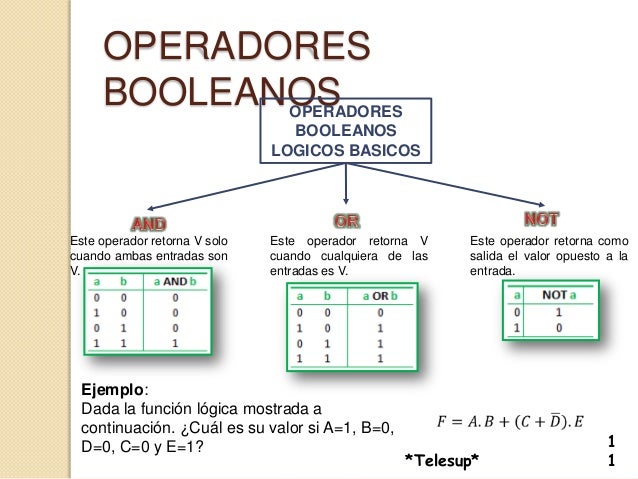
Álgebra de Boole en informática y matemática, son estructuras algebraicas que representan las operaciones lógicas AND (y; equivalente a la multiplicación), OR (ó; equivalente a la suma) y NOT (no; equivalente a la negación o complementación).

En electrónica digital (puertas lógicas) también se emplean la X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia) . En matemática a menudo se utiliza “+” en lugar de OR y “x” en lugar de AND, debido a que estas operaciones son de alguna manera análogas a la suma y el producto en otras estructuras algebraicas, y NOT se representa como una línea o una comilla sobre la expresión que se pretende negar (NO A sería Ā o A').

Se denomina así en honor a George Boole, matemático inglés que fue el primero en definirla como parte de un sistema lógico a mediados del siglo XIX. Específicamente, el álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica. En la actualidad el álgebra de Boole se aplica de forma generalizada en diseño electrónico de circuitos.

En conclusión, y por lo que yo he entendido después de investigar acerca de este tema, decir que: En el mundo de la electrónica, los valores que se utilizan son binarios, es decir, unos y ceros, donde el 1 significa que hay un valor determinado de voltaje de electricidad continua y 0 otro valor distinto, y decimos electricidad continua, porque hablamos de sistemas digitales. Asique desde la lógica y si tenemos la operación NOT, si entra un 0 sale un 1 y viceversa. En las dos operaciones restantes, tendríamos dos valores de entrada y uno de salida. En la operación AND, se tiene que dar la condición que el primer Y el segundo valor, sean iguales a 1, si se cumple, el resultado es uno, sino, es 0. O, dicho de forma matemática, sería el producto de los dos valores, 0x0=0, 0x1=0,1x0=0, y 1x1=1.